Kaspersky Password Manager: All of your passwords are belong to us

tl;dr: The password generator integrated in Kaspersky Password Manager had several concerns. Essentially the most serious one is that it ancient a PRNG now not suited to cryptographic functions. Its single source of entropy modified into once the unusual time. The final passwords it created might presumably perchance also very smartly be bruteforced in seconds. This article explains easy suggestions to safely generate passwords, why Kaspersky Password Manager failed, and uncomplicated suggestions to spend this flaw. It furthermore provides a proof of belief to take a look at if your version is inclined.

The product has been up prior to now and its most modern variations aren’t tormented by this discipline.

Introduction

Two years ago, we checked out Kaspersky Password Manager (KPM), a password manager developed by Kaspersky. Kaspersky Password Manager is a product that securely stores passwords and documents into an encrypted vault, safe by a password. This vault is safe with a master password, so, as with other password managers, users want to take into accout a single password to make spend of and put collectively all their passwords. Product is straight away available for diverse working methods (Home windows, macOS, Android, iOS, Web…) Encrypted recordsdata can then be robotically synchronized between your whole units, repeatedly safe by your master password.

The principle efficiency of KPM is password management. One key point with password managers is that, contrary to folks, these instruments are suitable to generate random, solid passwords. To generate stable passwords, Kaspersky Password Manager must rely on a stable password generation mechanism. We can first predict an instance of an appropriate password generation approach, to describe after why the approach ancient by Kaspersky modified into once wrong, and the draw in which we exploited it. As we are able to predict, passwords generated by this instrument will most likely be bruteforced in seconds.

After a tiny bit decrease than two years, this vulnerability has been patched on all variations of KPM. Vulnerability has been assigned CVE-2020-27020.

Producing principal passwords from a charset

For the sake of simplicity, let’s predict how passwords are generated in KeePass, an initiate source mission. Password generation is implemented in diverse lessons in the KeePassLib.Cryptography.PasswordGenerator namespace. KeePass provides 3 suggestions to generate a password: a charset-basically basically based, a sample-basically basically based and a personalized generation approach.

The less complicated approach is the charset-wicked generator, which creates a password from a given charset. Let predict how it truly works. Here is the principle loop in management of the password generation:

PwCharSet pcs = unusual PwCharSet(pwProfile.CharSet.ToString());
if(!PwGenerator.PrepareCharSet(pcs, pwProfile))
    return PwgError.InvalidCharSet;

char[] v = unusual char[pwProfile.Length];
try
{
    for(int i = 0; i < v.Length; ++i)
    {
        char ch = PwGenerator.GenerateCharacter(pcs, crsRandomSource);
        if(ch == char.MinValue)
            return PwgError.TooFewCharacters;

        v[i] = ch;
        if(pwProfile.NoRepeatingCharacters) pcs.Remove(ch);
    }
    ...
}

The GenerateCharacter method is called to generate every single character from the password. It takes a charset and a random source, and outputs a random character from the charset. Its implementation is rather straightforward:

internal static char GenerateCharacter(PwCharSet pwCharSet,
                                       CryptoRandomStream crsRandomSource)
{
    uint cc = pwCharSet.Size;
    if(cc == 0) return char.MinValue;

    uint i = (uint)crsRandomSource.GetRandomUInt64(cc);
    return pwCharSet[i];
}

Finally, GetRandomUInt64 is a uniform random number generator that outputs values between 0 and cc – 1:

internal ulong GetRandomUInt64(ulong uMaxExcl)
{
    if(uMaxExcl == 0) { Debug.Assert(false); throw new ArgumentOutOfRangeException("uMaxExcl"); }

    ulong uGen, uRem;
    do
    {
        uGen = GetRandomUInt64();
        uRem = uGen % uMaxExcl;
    }
    while((uGen - uRem) > (ulong.MaxValue - (uMaxExcl - 1UL)));
    // This ensures that the last quantity of the block (i.e.
    // (uGen - uRem) + (uMaxExcl - 1)) is generatable;
    // for signed longs, overflow to opposed quantity: 
    // whereas((uGen - uRem) + (uMaxExcl - 1) < 0);

    return uRem;
}

What is important here is that each character is generated independently from the other ones: every character is random, and knowing which character has been generated before does not give us information about the next char that will be generated.

Finally, let’s assume GetRandomUInt64 is cryptographically strong, and generates a random 64-bit number. Why is there a loop here, and why does this function is not simply implemented as return GetRandomUInt64() % uMaxExcl;?

Uniform random number generation

This loop is essential to uniformly generate numbers in a range.

Imagine you want to get a random char from a charset of 10 possible chars, and you have a random number generator method GetRandom32 which outputs number between 0 and 32 (32 excluded). The straightforward way to output such char would be:

const string charset = "0123456789";
return charset[GetRandom32() % 10];

Let’s see how characters are generated:

“4” is returned if GetRandom32() returns 4, 14 or 24 (3 possible values)
“5” is returned if GetRandom32() returns 5, 15 or 25 (3 possible values)
But “1” is returned if GetRandom32() returns 1, 11, 21 and 31 (4 possible values!)

The distribution is given below:

So there is a bias with this method: as one can see from the outputs, digits 0 and 1 will be output more frequently than the other ones. It is commonly called the “modulo bias”. You should check the excellent Definitive guide to “modular bias” and how to avoid it, by Kudelski Security, for more information.

To remove this “modulo bias”, a common method is to discard all the numbers greater than or equal to 30 (the biggest multiple of 10 lower than 16):

const string charset = "0123456789";
do {
    uGen = GetRandom32();
} while (uGen >= 30);
return charset[uGen];

This is precisely what KeePass does, though the bias in KeePass would be great much less fundamental than in the unusual instance, on story of the GetRandomUInt64 generates values great bigger than the scale of the password personality build.

We observed easy suggestions to uniformly exercise out a personality from a given fluctuate of characters, assuming our random source is uniform. Let’s predict now what extra or much less source is suitable to generate cryptographically solid random numbers.

Cryptographically stable PRNG

Generated numbers might presumably perchance also simply serene be random. But what does that mean precisely? A celebrated suitable PRNG will slump a chain of assessments, mainly statistical randomness assessments similar to Diehard or Dieharder assessments.

A cryptographically stable PRNG (CSPRNG) will furthermore slump these assessments, nonetheless it furthermore has two other requirements:

It must satisfy the next-bit take a look at. Incandescent the whole bits already generated by a CSPRNG, there might be not any polynomial-time approach that will predict the next bit with a chance elevated that 0.5.
If, at any moment, your whole grunt of the CSPRNG is compromised, there might be not any formula to retrieve the bits beforehand returned by the CSPRNG.

These components are very vital for password generation. To illustrate, if a password has been compromised for some motive, and if a non-CSPRNG has been ancient to generate this password, an attacker might presumably perchance also then be ready to retrieve the opposite password generated using this PRNG. Most working methods present CSPRNG implementations: CryptGenRandom on Home windows, or /dev/random on UNIX-relish working methods.

Some instrument lift to make spend of their very have implementation, on the whole seeded, fully or in part, by the working machine PRNG. KeePass makes spend of two PRNG, basically basically based either on Salsa20 and ChaCha20, and a legacy one per a variant of ARCFour. Let’s remove the major two PRNG are cryptographically stable: we have the whole parts to generate random, stable passwords from a given charset.

Kaspersky’s Password Abilities Approach

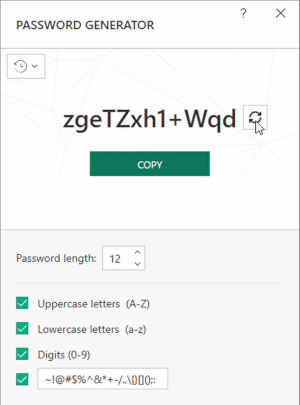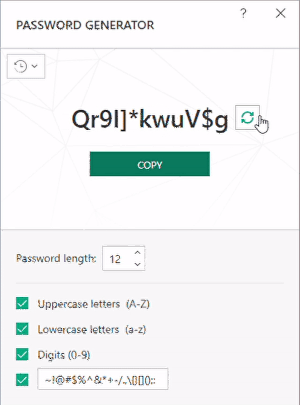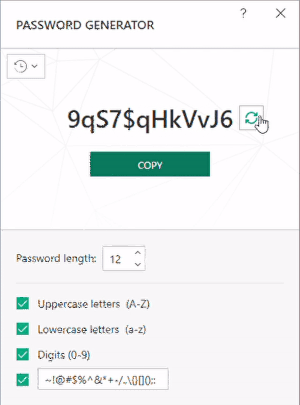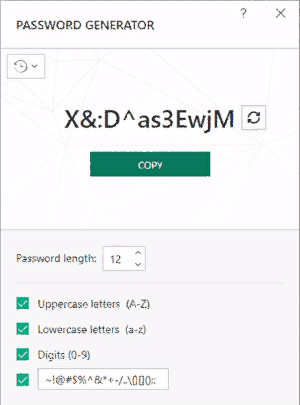
Kaspersky Password Manager has a built-in password generator, which creates password from a given “policy”. The policy settings are easy: password length, uppercase letters, lowercase letters, digits, and a personalized build of special chars. All these settings will most likely be configured in the Password generator interface, as confirmed here (here’s the celebrated surroundings):

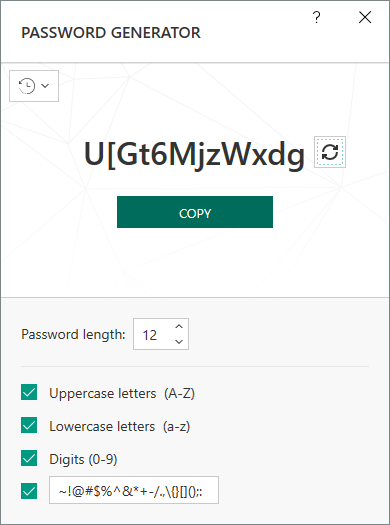
By default, KPM generates 12-personality passwords with a long charset.

Tricking the frequency of appearance

The generation draw is great extra complex than the Keepass approach. KPM first picks two random floats $r_1$ and $r_2$ between 0 and 1, and multiplies them with the length of the password charset to exercise a ticket in the charset table:

charset = ...  # personality build to make spend of
r1 = random.random()
r2 = random.random()
pos = r1 * r2 * len(charset)
return charset[pos]

The distribution of $r_1 times r_2$ is (thanks to MathWorld):

[begin{eqnarray} P[r_1 r_2 = a] &=& int_0^1int_0^1 delta(xy – a) dy dx \ &=& int_0^1int_{-a}^{x-a} delta(z) frac{1}{x} dz dx \ &=& int_0^1 1(x geq a) frac{1}{x} dx \ &=& int_a^1 frac{1}{x} dx \ &=& -ln(a) terminate{eqnarray}]

Let’s plight it:

The distribution of this selection is now not uniform: decrease positions have extra potentialities to occur than values terminate to from 1. Such approach is rather puzzling, nonetheless it appears it’s precisely what KPM desired to implement.

How is created the charset? Is it fully ordered, relish “abcdefghij…”? No…

For the major three chars, charset is fully ordered (nearly… we are able to predict that later).
Then, for the next chars, KPM depends on letter frequency: it assumes least frequent letters (in some language) might presumably perchance also simply serene appear extra on the whole in the generated password. The supposed frequency of apparition of every letter, as ancient in KPM, is confirmed in the graph below:

Then, charset is ordered per the inverse frequency of appearance of every letter: q, x, z, w… n, a, e.

As decrease values in most cases have a tendency to appear given the distribution feature, we can remove some chars relish “q” and “x” in most cases have a tendency to appear in passwords generated by KPM.

If these stats had been taken independently to generate every char of a password, we might presumably perchance also predict on the whole several “q”, “x” or “z” in the passwords. On the opposite hand, things are extra complex: generated chars are taken into story in the computation of the frequencies of appearance. If a “z” is generated, then the prospect of appearance of “z” in the frequency table will most likely be strongly elevated. As soon as the charset is ordered per this table, “z” will most likely be at the terminate of the table, and might presumably perchance well simply have great much less modifications to be taken.

These modifications furthermore impact other letters: after “z” has been picked, the prospect of “a”, “e”, “m”, “q”, “s” and “x” has furthermore elevated. Quite the opposite, “h” has lowered. But, after “h” is picked, its chance of appearance will then impact bigger so a lot.

Our hypothesis is that approach has been implemented to trick celebrated password cracking instruments. Password crackers similar to Hashcat or John the Ripper try to spoil first probable password, e.g. passwords generated by folks. Their password cracking approach depends on the truth that there are doubtlessly “e” and “a” in a password created by a human than “x” or “j”, or that the bigrams “th” and “he” will appear great extra on the whole than “qx” or “zr”.

Devoted tactics similar to Markov generator, which remove that there might be a hidden Markov model in the approach passwords are generated by folks, can straight spoil this approach of generation (predict Like a flash Dictionary Assaults on Passwords Utilizing Time-Space Tradeoff for added info).

Therefore, passwords generated by KPM will most likely be, on sensible, far in the checklist of candidate passwords examined by these instruments. If an attacker tries to crack a listing of passwords generated by KPM, he’ll doubtlessly wait rather a in point of fact lengthy time until the major one is learned. This is rather artful.

On the opposite hand, if an attacker knows that a password has been generated by KPM, he can adapt his instrument to grasp into story the model followed by KPM. As these passwords are, in a definite sense, biased (to style out password crackers), this bias will most likely be ancient to generate basically the most probable passwords generated by this instrument, and take a look at them first. A easy formula to attain it can presumably perchance well also very smartly be to make spend of a Markov generator, as the one equipped by John the Ripper (This approach has now not been examined).

We can attain that the generation algorithm in itself is now not that wicked: it ought to resist against celebrated instruments. On the opposite hand, if an attacker knows a person makes spend of KPM, he’ll be ready to spoil his password great extra without relate than a fully random password. Our recommendation is, on the other hand, to generate random passwords lengthy ample to be too solid to be broken by a instrument.

We beforehand observed that KPM picked two random values $r_1$ and $r_2$ to compute an index in the charset table. Let’s predict now how these values are computed.

KPM’s Random Quantity Generator

These two values come straight from the KPM PRNG. This PRNG outputs uniformly floats between 0 and 1, 1 excluded.

The PRNG ancient differs in the Desktop and the Web version:

The Web version ancient Math.random(). This selection is now not suitable to generate cryptographically stable random numbers (which contains entropy required to generate passwords), as defined in https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Math/random. The underlying PRNG ancient by Chrome, Firefox and Safari for Math.random() is xorshift128+. It’s very mercurial, but now not suitable to generate cryptographic discipline cloth. The protection consequences in KPM has now not been studied, but we informed Kaspersky to interchange it with window.crypto.getRandomValues(), as urged by the Mozilla documentation page beforehand talked about.
The desktop version ancient a PRNG equipped by Boost: the mt19937 Mersenne Twister. Mersenne Twister is extremely suitable and broadly ancient PRNG, and MT 19937 is the most unusual Mersenne Twister. It’s uniformly disbursed, has a in point of fact lengthy duration, and is mercurial when in contrast to the opposite “suitable” PRNGs.

On the opposite hand, is using a Mersenne Twister an appropriate recommendation to fabricate passwords? Truly now not.

The topic with this generator is that it’s now not a CSPRNG. Incandescent a pair of of its ouputs (624 if this is the case) enables to retrieve its elephantine grunt, and to predict the whole values it ought to generate, plus the whole values it has already generated (predict Berlekamp-Massey or Reeds-Sloane algorithms).

Off-the-shelf instruments relish randcrack are readily available to spoil Python’s random module, which makes spend of a in point of fact same (if now not the same) implementation of MT 19937. Most piquant very minor variations might presumably perchance also simply serene be necessary to spoil Boost implementation.

In put collectively, exploiting such flaw in the context of Kaspersky’s Password Manager is difficult:

Passwords are fast: 12 chars by default. Retrieving 624 password chars requires to grasp 52 passwords.
The raw output worth is now not identified: output worth is the situation in the charset of every letter of the password. More values might presumably perchance also very smartly be necessary.
And we observed that this case in the charset is a the manufactured from two values produced by the PRNG.

We attain now not predict a easy formula to assault this PRNG in the context of KPM.

Seeding the Mersenne Twister

We observed that the PRNG uniformly generates floats in [0, 1[. The code in management of its initialization might presumably perchance also simply serene witness relish:

mt19937:: result_type seed = ...;
auto mtrand = std:: bind(std:: uniform_real_distribution<float>(0,1), mt19937(seed));

Where does the seed come from? The password generation feature is is assumed as relish this:

std:: string pwlib:: generatePassword(pwdlib:: Protection policy, int seed)
{
    if (seed == 0) {
        FILETIME ft;

        GetSystemTimeAsFileTime(&ft);
        seed = ft.dwLowDateTime + ft.dwHighDateTime;
    }
    auto mtrand = std:: bind(std:: uniform_real_distribution<float>(0,1), mt19937(seed));
    return generateRandomPassword(policy, mtrand);
}

This is mammoth piquant for two causes:

The seed is suitable 32 bits. Which draw it ought to be bruteforced without relate.
An instance of the PRNG is created each time a password is generated. It draw Kaspersky Password Manager can generated at most $2^{32}$ passwords for a given charset.

GetSystemTimeAsFileTime is ancient as a seed easiest if a seed is now not equipped to the generatePassword approach. How is is assumed as this approach when a user requests a unusual password? The acknowledge is:

std:: string pwlib:: generatePassword(pwdlib:: Protection policy)
{
  return generatePassword(policy, time(0));
}

So the seed ancient to generate every password is the unusual machine time, in seconds. It draw every instance of Kaspersky Password Manager on the planet will generate the very same password at a given second. This might occasionally be glaring to build if every click on the “Generate” button, in the password generator interface, produced the same password. On the opposite hand, for some motive, password generation is challenging: dozens of random chars are displayed whereas the right password has already been computed:

This animation takes bigger than 1 second, so it’s now not imaginable to click several times on the “Generate” button within a second. That’s definitely why the weak point had now not been learned sooner than.

The implications are obviously wicked: every password might presumably perchance also very smartly be bruteforced. To illustrate, there are 315619200 seconds between 2010 and 2021, so KPM might presumably perchance also generate at most 315619200 passwords for a given charset. Bruteforcing them takes a pair of minutes.

It’s rather frequent that Web sites or forums describe the introduction time of accounts. Incandescent the introduction date of an story, an attacker can try to bruteforce the story password with a limited fluctuate of passwords (~100) and make glean correct of entry to to it.

Moreover, passwords from leaked databases containing hashed passwords, passwords for encrypted archives, TrueCrypt/Veracrypt volumes, etc. will most likely be furthermore without relate retrieved if they had been generated using Kaspersky Password Manager.

An unexpected source of entropy: out-of-bounds read

We wrote a proof of belief to be definite we had been now not lacking one thing. It generates a listing of 1000 imaginable passwords from the unusual time. To study the PoC:

Bring collectively the equipped PoC (pwlib.cpp). File might presumably perchance also simply serene be compiled with Visual C++ (floating values in the source code have now not the very same values when compiled with Clang or gcc). I ancient Visual C++ 2017 for my assessments. Utilizing a uncover invite for Visual C++ 32 bits, enter:
```
 cmake -Bbuild -H.
 msbuild makepwbrute.vcxproj
```
Tear compiled executable to fabricate a listing of 1000 passwords.
```
 Debugpwbrute.exe > slump.txt
```
Make a password in Kaspersky Password Manager with the next policy:
- Lowercase easiest
- 12 chars
Verify that the generated password is certainly fresh in slump.txt.

It’s now not totally purposeful, but allowed us to deem a computer virus in the password generation course of, in the feature that computes the prospect of appearance of a given letter shiny the beforehand generated chars. Here is the pseudo code for the getContextProbabilities approach:

  const drift *getContextProbabilities(const std:: string &password) {
    std:: string lowercasePassword;

    // Convert to lowercase, be pleased easiest lowercase
    for (char c :  password) {
      if (islower(c)) {
        lowercasePassword += c;
      } else if (isupper(c)) {
        lowercasePassword += char(c - 'A' + 'a');
      }
    }
...
    int n = 0;
    for (int i = lowercasePassword.length() - 1; i >= 0; i--) {
      int index = password[i] - 'a'; // FIXME: change with lowercasePassword

The password being built is converted to lowercase. Non-letters are removed. Then, there might be an iteration on the password in situation of the lowercase password suitable created. This results in a contaminated computation of the index variable (the situation of a letter in the alphabet). This index is ancient to retrieve an element of an array. That results in an out-of-bounds read of this array.

Frequency of appearances are then computed from uninitialized or arbitrary recordsdata in some cases. Though the algorithm is contaminated, it truly makes the passwords extra refined to bruteforce in some cases.

The attacked PoC generates candidates for lowercase passwords easiest in order that the index is repeatedly accurately computed (else the PoC requires to be tailored).

Kaspersky assigned CVE-2020-27020 to this vulnerability, and printed a security advisory on their online page: https://give a boost to.kaspersky.com/overall/vulnerability.aspx?el=12430#270421.

The final variations previous to these ones are affected:

Kaspersky Password Manager for Home windows 9.0.2 Patch F
Kaspersky Password Manager for Android 9.2.14.872
Kaspersky Password Manager for iOS 9.2.14.31

On Home windows, the Mersenne Twister PRNG has been modified with the BCryptGenRandom feature:

drift RandomFloat(BCRYPT_ALG_HANDLE *hAlgorithm) {
    uint32_t l;
    BCryptGenRandom(*hAlgorithm, (uint8_t *)&l, sizeof(l), 0);
    return (drift)l * (1.0f / 0x100000000);
}

The return worth of this selection modified into once now not checked in the beta variations equipped by Kaspersky, but we guess this has been mounted now.

Math.random() in the Web version has been modified with the stable window.crypto.getRandomValues() approach.

Android and iOS variations have furthermore been patched, but we have now not checked out the fixes.

Conclusion

Kaspersky Password Manager ancient a elaborate formula to generate its passwords. This approach aimed to fabricate passwords hard to spoil for celebrated password crackers. On the opposite hand, such approach lowers the energy of the generated passwords against dedicated instruments. We showed easy suggestions to generate stable passwords taking KeePass as an illustration: easy suggestions relish random attracts are stable, as soon as you glean rid of the “modulo bias” whereas peeking a letter from a given fluctuate of chars.

We furthermore studied the Kaspersky’s PRNG, and showed it modified into once very worn. Its internal development, a Mersenne twister taken from the Boost library, is now not suited to generate cryptographic discipline cloth. But the major flaw is that this PRNG modified into once seeded with the unusual time, in seconds. Which draw every password generated by inclined variations of KPM will most likely be bruteforced in minutes (or in a second whereas you occur to grasp roughly the generation time).

At last, we equipped a proof of belief that info the elephantine generation approach ancient by KPM. It will seemingly be ancient to analysis the flaw is certainly fresh in Home windows variations of Kaspersky Password Manager < 9.0.2 Patch F. By the draw in which, penning this PoC allowed us to build an out of bounds read all around the computation of the frequency of appearance of password chars, which makes passwords a tiny bit stronger that they'll also simply serene were.

Timeline

June 15, 2019: document and proof of belief sent to Kasperky via HackerOne.
June 17, 2019: Kaspersky acknowledges it has got the document.
June 25, 2019: Kaspersky confirms the vulnerability.
October 4, 2019: Kaspersky sends a non-public Home windows make so we can analysis the bugs were mounted, and informs us they are going to rollout a formula to cope with beforehand generated passwords sooner than the terminate of the year.
October 8, 2019: we direct the vulnerabilities were mounted, but reported a unusual limited defect in the repair.
October 10, 2019: Kaspersky Password Manager for Home windows 9.0.2 Patch D is released, fixing the vulnerabilities, but without the repair for the reported defect. Web version is furthermore up prior to now.
October 9, 2019: Kaspersky Password Manager for Android version 9.2.14.872 with the repair is released.
October 10, 2019: Kaspersky Password Manager for iOS version 9.2.14.31 with the repair is released.
December 10, 2019: Kaspersky Password Manager for Home windows 9.0.2 Patch F is released closing the defect in patch D.
April 9, 2020: Kaspersky informs us they are going to release a patch in October to cope with beforehand generated passwords.
October 13, 2020: Kaspersky Password Manager 9.0.2 Patch M is released, with a notification to users to repeat them some password might presumably perchance also simply serene be re-generated. Kaspersky informs us the same notification will furthermore be fresh in mobile variations all around the major quarter of 2021. CVE-2020-27020 has furthermore been reserved.
December 28, 2020: Kaspersky has the same opinion a document referring to the vulnerability will most likely be disclosed after the CVE is printed.
April 27, 2021: Kaspersky security advisory is printed.
Can also simply 14, 2021: Data for the CVE-2020-27020 is printed.

Kaspersky Password Manager: All of your passwords are belong to us

Introduction

Producing principal passwords from a charset

Uniform random number generation

Cryptographically stable PRNG

Kaspersky’s Password Abilities Approach

Tricking the frequency of appearance

KPM’s Random Quantity Generator

Seeding the Mersenne Twister

An unexpected source of entropy: out-of-bounds read

Conclusion

Timeline

Jirnal

Breaking Free from a “9 to 5” Tradition

‘Hot initiate’ concept says Pluto as soon as had a surface ocean

Introduction

Producing principal passwords from a charset

Uniform random number generation

Cryptographically stable PRNG

Kaspersky’s Password Abilities Approach

Tricking the frequency of appearance

KPM’s Random Quantity Generator

Seeding the Mersenne Twister

An unexpected source of entropy: out-of-bounds read

Conclusion

Timeline

Jirnal

Related Posts

What to peek in a CRT observe: The final info for retro gamers

GeForce RTX 3060 vs. Radeon RX 6600: Which GPU ought to you pick?

‘We’re willing to are attempting all the pieces’: How a startup snack value is leveraging meme culture to reach possibilities

‘Hot initiate’ concept says Pluto as soon as had a surface ocean