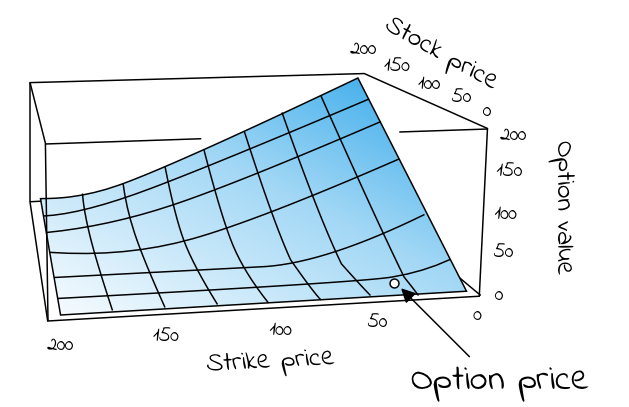
The Dim-Scholes formula explained with TSLA instance

The Dim–Scholes model is a mathematical model simulating the dynamics of a monetary market containing by-product monetary devices. Since its introduction in 1973 and refinement within the 1970s and 80s, the model has become the de-facto identical old for estimating the label of stock alternatives. The important thing notion within the support of the model is to hedge the alternatives in an investment portfolio by making an try for and selling the underlying asset (similar to a stock) in just the true formula and as a outcome, receive rid of probability. The formula has later become identified interior finance as “frequently revised delta hedging”, and been adopted by most of the enviornment’s predominant investment banks and hedge funds.

The aim of this text is to reward the Dim-Scholes equation’s mathematical foundation, underlying assumptions and implications.

Pleased learning!

The Dim–Scholes model is a mathematical model simulating the dynamics of a monetary market containing by-product monetary devices similar to alternatives, futures, forwards and swaps. The important thing property of the model is that it shows that an choice has a particular label no matter the probability of the underlying security and its expected return. The model is per a partial differential equation (PDE), the so-called Dim-Scholes equation, from which one can deduce the Dim-Scholes formula, which gives a theoretical estimate of one of the best likely label of European stock alternatives.

Assumptions

The distinctive Dim-Scholes model is per a core assumption that the market contains at the very least one unhealthy asset (similar to a stock) and one (in actual fact) probability-free asset, similar to a cash market fund, cash or a authorities bond. Moreover, it assumes three properties of the 2 property, and four of the market itself:

• Assumptions about the property within the market are: 1. The flee of return on the probability-free asset is continuous (thus effectively behaves as an hobby rate); 2. The instantaneous log return of the unhealthy asset’s label is notion to behave as an infinitesimal random stroll with fixed drift and volatility, more precisely, per geometric Brownian motion. 3. The unhealthy asset would no longer pay a dividend.
• Assumptions about the market itself are: 1. There don’t seem like any arbitrage (probability-free profit) opportunities; 2. It is doable to borrow and lend any amount of cash at the identical rate as the hobby rate of the probability-free asset; 3. It is doable to desire and sell any amount of the stock (in conjunction with short selling); and 4. There don’t seem like any transaction prices within the market (i.e. no commission for making an try for or selling securities or by-product devices).

In subsequent extensions of the distinctive model, these assumptions were revised to alter for dynamic hobby rates for the probability-free asset (Merton, 1976), transaction prices for making an try for and selling (Ingersoll, 1976) and dividend payouts for the unhealthy asset (Whaley, 1981). On this essay, make a selection we’re working with the distinctive model, unless said in any other case.

The Dim-Scholes equation is the partial differential equation (PDE) that governs the label evolution of European stock alternatives in monetary markets working per the dynamics of the Dim-Scholes (veritably Dim-Scholes-Merton) model. The equation is:

Where V is the label of the choice (as a feature of two variables: the stock label S and time t), r is the probability-free hobby rate (mediate hobby rate the same to that which that it’s likely you’ll presumably receive from a cash-market fund, German authorities debt or the same “safe” debt securities) and σ is the volatility of the log returns of the underlying security (for the functions of this text, we’re brooding about shares). A whimsical derivation of the equation is readily available on Wikipedia, per John C. Hull’s “Option, Futures and Other Derivatives” (1989).

If we rewrite the equation to the next invent

Then the left facet represents the commerce within the fee/label of the choice V due to time t increasing + the convexity of the choice’s fee relative to the label of the stock. The true hand facet represents the probability-free return from a protracted space within the choice and a short space consisting of ∂V/∂S shares of the stock. In the case of the greeks:

The important thing commentary of Dim and Scholes (1973) become once that the probability-free return of the blended portfolio of shares and alternatives on the true hand facet over any infinitesimal time interval can even very smartly be expressed as the sum of theta (Θ) and a duration of time incorporating gamma (Γ). The commentary is veritably identified as the “probability neutral argument”. This since the fee of theta (Θ) is regularly damaging (since the fee of the choice decreases as time moves closer to expiration) and the fee of gamma (Γ) is regularly obvious (reflecting the gains the portfolio receives from conserving the choice). In sum, the losses from theta and the gains from gamma offset every other, main to returns at a probability-free rate.

The Dim-Scholes formula is a design to the Dim-Scholes PDE, given the boundary prerequisites below (eq. 4 and 5). It calculates the label of European put and receive in touch with alternatives. That is, it calculates the label of contracts for the true (nonetheless no longer obligation) to desire or sell some underlaying asset at a pre-particular label on a pre-particular date at some point. At maturity/expiration (T), the fee of such European name (C) and put (P) alternatives are given by, respectively:

Dim and Scholes confirmed that the purposeful invent of the analytic design to the Dim-Scholes equation (eq. 1 above) with the boundary prerequisites given by eq. 4 and 5, for a European name choice is:

The formula gives the fee/label of European name alternatives for a non-dividend-paying stock. The components going into the formula are S = label of security, T = date of expiration, t = most new date, X = affirm label, r = probability-free hobby rate and σ = volatility (identical old deviation of the underlying asset). The feature N(・) represents the cumulative distribution feature for a typical (Gaussian) distribution and shall be notion to be as ‘the probability that a random variable is much less or equal to its input (i.e. d₁ and d₂) for a typical distribution’. Being a probability, the of fee N(・) in other phrases will frequently be between 0 ≤ N(・) ≤ 1. The inputs d₁ and d₂ are given by:

Very informally, the 2 terms within the sum given by the Dim-Scholes formula will be notion to be as ‘the most new label of the stock weighted by the probability that you are going to affirm your choice to desire the stock’ minus ‘the discounted label of exercising the choice weighted by the probability that you are going to affirm the choice’, or merely ‘what you are going to receive’ minus ‘what you are going to pay’ (Khan, 2013).

For a European put choice (contracts for the true, nonetheless no longer obligation, to sell some underlaying asset at a pre-particular label on a pre-particular date at some point) the the same purposeful invent is:

Example: Calculating the label of a European name choice

In account for to calculate what the label of a European name choice ought to be, we all know we need 5 values required by equation 6 above. They are: 1. The most new label of the stock (S), 2. The affirm label of the resolution choice (X), 3. The time to expiration (T – t), 4. The probability-free hobby rate (r) and 5. The volatility of the stock, given by the common deviation of historical log returns (σ).

Estimating the fee of a name choice for Tesla (TSLA)

The first four values we need are with out peril within the market. Let’s disclose we're attracted to a name choice for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a label 20% elevated than the stock is at reward shopping and selling.  Tesla’s NASDAQ list ($TSLA) on Yahoo Finance lately (July 13th, 2019), we discover a stock label of S = $245. Multiplying the most new label with 1.2 gives us an affirm label 20% elevated than the stock is at reward shopping and selling, X = $294. Googling, we discover that the day of its Q3 earnings name is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a probability-free hobby rate instrument, we’ll exhaust US 10-12 months authorities bonds ($USGG10YR), at reward paying off 2.12%.So, we discover S = 245, X = 294, T - t = 101 and r = 0.0212. The handiest lacking fee is an estimation of the stock’s volatility (σ).

We are in a position to estimate any stock’s volatility by gazing its historical prices, or, even more efficient, by calculating other choice prices for the identical stock at various maturity/expiration dates (T) and affirm/strike prices (X), if we all know they’ve been situation per a Dim-Scholes model. The resulting fee, σ, is a bunch between 0 and 1, representing the market’s implied volatility for the stock. For Tesla, at the time of writing this text, the fee averaged at approximately 0.38 for 4–5 various choice prices around the identical expiry/maturity date. Enter into equation 6 above, we discover that the resolution choice we’re attracted to ought to be prices somewhere around $7.

Implied volatility

Even supposing it is difficult to non-public how alternatives issuers approach at the label of their name and put alternatives, as traders it’s traumatic to “disagree” with such prices, per se, and so traumatic to turn this records into actionable investment theses.

We are in a position to nonetheless receive more than a number of milage out of the Dim-Scholes formula if we as a exchange care for the label of an choice (C or P) as a identified amount/just variable (chanced on by having a glance at various maturity/expiration dates T and various affirm prices X). This which potential of, if we develop, the Dim-Scholes purposeful equation turns correct into a instrument to lend a hand us realize how the market estimates the volatility of a stock, veritably identified as the implied volatility of the choice. Here is records we can disagree over, and commerce in opposition to.

Hypothetical location

If we for instance learn about at the chart for the Tesla stock over the closing three months (resolve 2), we seek a fairly (for a lack of the next word) unsafe inch from hovering around $280 three months ago, to a low of $180 a month and a half of ago, to now on its formula support up at $245. This makes sense given the volatility we noticed from name prices sooner than ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It would no longer compose sense, nonetheless, if we mediate the fluctuation over the past three months become once the mere tip of an iceberg, going correct into a duration of more volatility for Tesla, disclose, due to an upcoming enlarge in short-selling.

Let's disclose we disagree with an alternatives issuer about the implied volatility of stock's efficiency over the closing three months. We mediate the lunge is going to receive rockier. How grand? Let's disclose that as a exchange of 40%, we mediate the next three months will learn about more fancy 60%. Enter into the purposeful Dim-Scholes formula alongside with the identical values for S, X, r, and T - t, we receive a label of virtually twice of what the alternatives issuer needs, at C(S,t) = $14.32. This we can commerce on. We would possibly perchance well, for instance, lift name alternatives lately and no longer sleep for volatility to enlarge or the fee of the stock to head up, sooner than selling at a profit.

Because American alternatives will also be exercised at any date sooner than expiration (so-called “continuous timeline devices”), they are device more traumatic to take care of that European alternatives (“deadline devices”). Primarily, since the optimal affirm policy can hang an affect on the fee of the choice, this must be taken into story when fixing the Dim-Scholes partial differential equation. There don’t seem like any identified “closed invent” solutions for American alternatives per the Dim-Scholes equation. There are, though, some special conditions:

• For American name alternatives on underlying property that develop no longer pay dividend (or other payouts), the American name choice label is the identical as for European name alternatives. This since the optimal affirm policy on this case is to no longer affirm the choice.
• For American name alternatives on underlying property that develop pay one identified dividend in its lifetime, it will possibly be optimal to affirm the choice early. In such conditions the choice will be optimally exercised correct sooner than the stock goes ex-dividend, per a solution given in closed-invent by the so-called Roll-Geske-Whaley device (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

First, test if it is optimal to affirm the choice early, by investigating whether the next inequality is fulfilled:

For S = stock label, X = affirm label, D₁ = dividend paid, t = most new date, t₁ = date of dividend fee, T = expiration date of choice.

If the inequality is no longer fulfilled, early affirm it no longer optimal. If C(・) is the common Dim-Scholes formula for European name alternatives on non-dividend-paying stock (eq x), the fee of the American name choice is then given by a model of the identical equation the establish the stock label (S) is discounted:

If the inequality is fulfilled, early affirm is optimal and the fee of the American name choice is given by the next, dreadful, mess of an equation (I attempted to interrupt it up by whenever duration to compose it more readable):

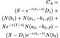
Where as sooner than S = label of stock, T = date of expiration of choice, X = affirm label and r = probability-free hobby rate, σ = volatility (identical old deviation of the log of the historical returns of the stock), and D₁ is the dividend payout. Moreover, ρ is given by:

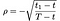
a₁, a₂ by:

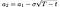
and b₁, b₂ by:

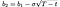
It will head with out announcing that Dim-Scholes model is precisely that, a theoretical model that tries to estimate how a market behaves, given the assumptions said above and the inherent limitations of our luxuriate in numerical estimations of probability-free hobby rates (r) and future volatility (σ). It will here be highlighted that no longer the full assumptions of (specifically the distinctive model) are in actual fact empirically genuine. As an instance, critical limitations come up from:

• The underestimation of rude moves within the stock, yielding tail probability
• The assumption of rapid, label-much less shopping and selling, yielding liquidity probability
• The assumption of a stationary job, yielding volatility probability
• The assumption of continuing time and shopping and selling, yielding gap probability

These ought to be accounted for in any and all investment systems, for instance by hedging with out-of-the-cash alternatives, shopping and selling on loads of exchanges, hedging with volatility hedging and Gamma hedging, respectively.

As fleet talked about it become once Fischer Dim and Myron Scholes who in 1973 confirmed that dynamically revising a portfolio per obvious guidelines eliminates the expected return of the underlying security (Dim & Scholes, 1973). Their model built on beforehand established works by Bachelier, Samuelson and others. Robert C. Merton become once the first to post a paper increasing on the understanding of the model and who coined the duration of time “Dim-Scholes alternatives pricing model”. Scholes and Merton become once awarded the 1997 Nobel Memorial Prize in Economic Sciences for their discovery of the vogue of divorcing stock alternatives from the probability of their underlying securities. As Fischer Dim handed away in 1995, he would no longer be eligible to receive the award, nonetheless become once acknowledged as a contributor by the Nobel Academy.