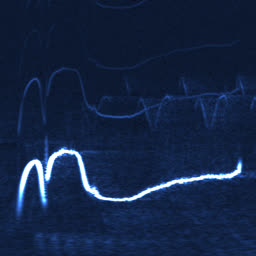
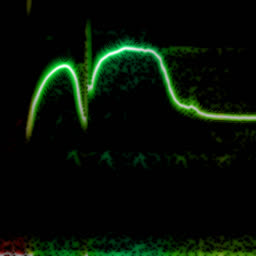
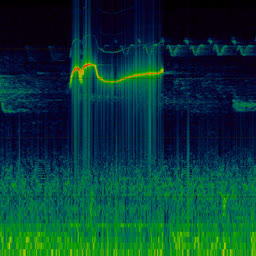
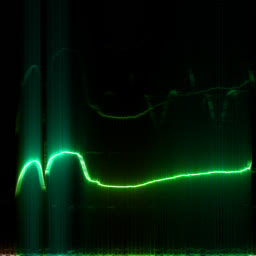
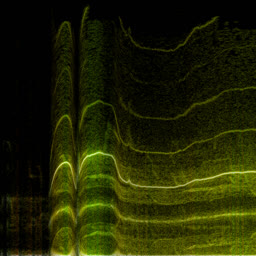
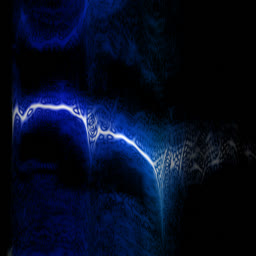
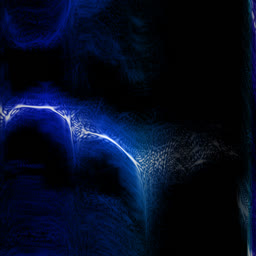
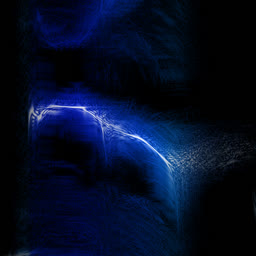
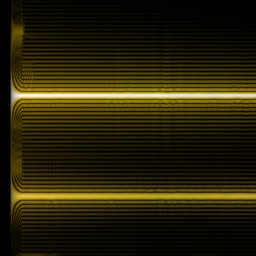
Analysing chook songs with Wigner transform (WDF)

GitHub: soundshader.github.io

Demo: soundshader.github.io/hss?wdf=1

You’ll want to skillfully employ WASD and QERF keys to circulation around and zoom-in/zoom-out.

As I used to be buying for piquant audio transforms, I came across the Wigner distribution characteristic (or lawful WDF). The instance on Wikipedia seems indeed piquant and it’s “sold” as a characteristic that “supplies the most practical that that you just can perchance perchance also deem temporal vs frequency resolution which is mathematically that that you just can perchance perchance also deem contained in the obstacles of the uncertainty precept” and thus “when a signal is no longer time restricted, its WDF is exhausting to implement.” Looks, WDF isn’t grand extra difficult to implement than undeniable FFT.

The definition of WDF is this:

It does an piquant trick: at every time limit it inverts the audio signal and multiplies it by its long-established time-ahead model. That is shining on chronicle of a periodic signal at time T would in the neighborhood correlate with a time inverted model of itself, nonetheless in WDF this correlation isn’t time bounded, so if the signal is 1 hour lengthy, WDF will multiply two one hour lengthy alerts to compute lawful one fee at T. This seems meaningless first and most most principal gape, as the random contributions 30 mins some distance from the recent second would form WDF random, nonetheless a more in-depth watch unearths that if these some distance-off contributions are indeed random, they would end out each and every assorted, and they also invent out (to an extent). The complicated exponent on the honest is successfully the identical outdated FFT on the ahead-inverted correlation.

In apply, this kind a easy algorithm to compute WDF:

1. Private N samples on the recent second: x[1..N]
2. Practice the Hann window to approximate cancellation of some distance-away terms.
3. Multiply it by the reversed reproduction of itself: y[1..N] = x[1..N] x[N..1]
4. Stretch it to chronicle for x(t+tau/2) in the system above: y[1..N/2] -> z[1..N]
5. Compute the identical outdated Z = FFT[z]

So it doesn’t in actuality add any complexity on top of the long-established FFT. In apply, although, WDF is a critically noisy characteristic that’s grand much less insightful than undeniable FFT. Below is the an identical chook recording (xeno-canto.org/33539) visualized with assorted ideas.

1. CWT with the Morlet wavelet.
2. FFT with the Hann window characteristic. Right here’s practically an equivalent to CWT, as the latter is extra or much less the an identical as FFT with the a tiny bit assorted Gaussian window. And unlike CWT, computing FFT doesn’t involve any mental gymnastics.
3. Undeniable FFT spectrogram with 1024 boxes at 48 kHz. Pixelated on chronicle of handiest 300 or so boxes gather the critical 0..8 kHz differ.
4. “Continuous FFT” spectrogram that makes employ of the DFT Shift Theorem and the identical outdated rectangular window characteristic which produces these sinc-formed diffraction patterns.
5. WDF with the Hann window on 2048 samples per frame.

WDF is ready to form piquant spectrograms as soon as rapidly, nonetheless usually it’s unusably noisy. Unlike FFT spectrograms, WDF will get extra staunch on elevated dwelling windows: frequency lines win thinner, on the expense of including extra noise around them. Below is the an identical violin pattern: an FFT spectrogram, and two WDF spectrograms with 2048 and 4096 samples per frame.

Some chook examples: WDFs with 2048, 4096 and 8192 samples per frame.

For some reason WDF is miles ahead on easy tibetian bowl sounds (that flip out to be no longer that straightforward). Right here’s the an identical 500 ms of sound, the 0..3 kHz differ (employ ?wdf=1&alog=3&boxes=4096 args):

A pair of extra bowl examples (all WDF):

Appendix

I’ve unintentionally came across that a sluggish ffmpeg -i chook.mp3 chook.ogg produces audio artifacts. Regardless that they are inaudible, they’ll also also be without problems viewed on spectrograms.

The fashioned mp3 (libvorbis) and transcoded ogg (default libvorbis, -compression_level 10):

Transcoded ogg (default libopus, -b:a 48k, -b:a 48k -compression_level 10 and lawful -compression_level 10):

The piquant conclusion is that specifying the honest bitrate (48k) achieves the very most piquant quality and the smallest file measurement as a bonus. Even the further “handiest compression” risk has no visible pause. Correct -compression_level 10 produces artifacts, as ffmpeg sets bitrate to 64k for some reason. I couldn’t win -codec:a libvorbis to form a lawful result. It need to work by hook or by crook as libvorbis is frail in the mp3 file, nonetheless I couldn’t figure the honest space of ffmpeg alternatives. Right here’s the winner issue line:

ffmpeg -i XC33539.mp3 -codec:a libopus -b:a 48k XC33539.ogg